Meet Mathematician Clayton Shonkwiler

Intended Audience: Everyone, and especially teachers who want to show to their students a mathematician explaining the motivation behind their own research.

In this episode we meet Clayton Shonkwiler, a mathematician from Colorado State University, who talks to us about applications of geometry and topology to the study of random polygons and polymer science.

Clayton discusses some ideas related to his paper with Jason Cantarella and Tetsuo Deguchi, Probability Theory of Random Polygons from the Quaternionic Viewpoint. Here is the first paragraph of the abstract to their paper.

We build a new probability measure on closed space and plane polygons. The key construction is a map, given by Knutson and Hausmann using the Hopf map on quaternions, from the complex Stiefel manifold of 2-frames in n-space to the space of closed n-gons in 3-space of total length 2. Our probability measure on polygon space is defined by pushing forward Haar measure on the Stiefel manifold by this map. A similar construction yields a probability measure on plane polygons which comes from a real Stiefel manifold.

While the video above is for a general audience, Clayton’s paper is not (it’s written for other mathematicians). However, ambitious high-school students may still enjoy looking at it to see what advanced theorems and proofs look like.

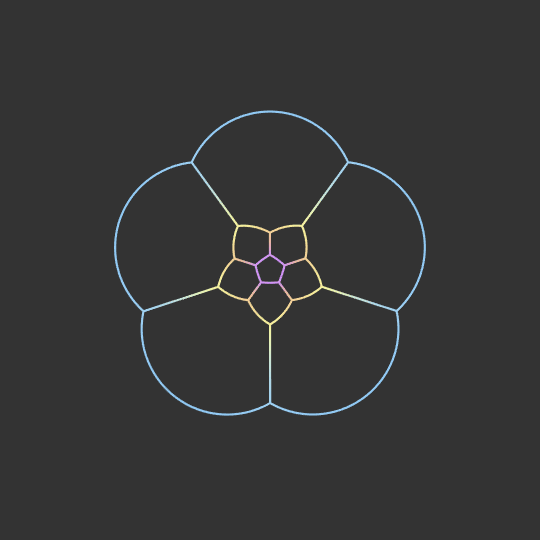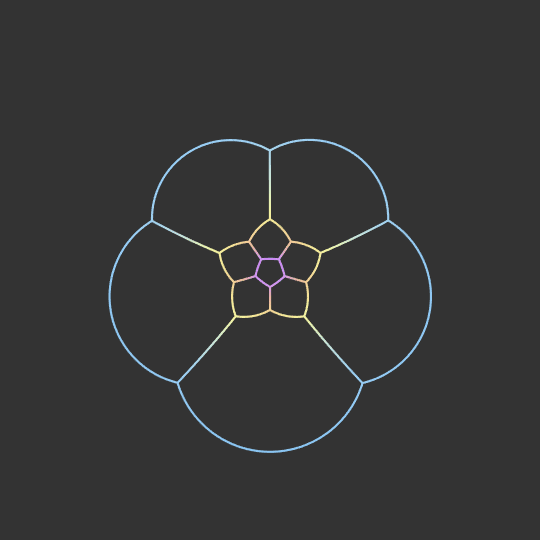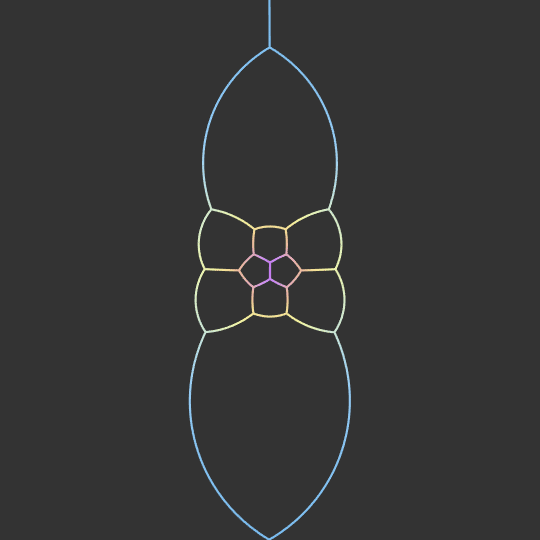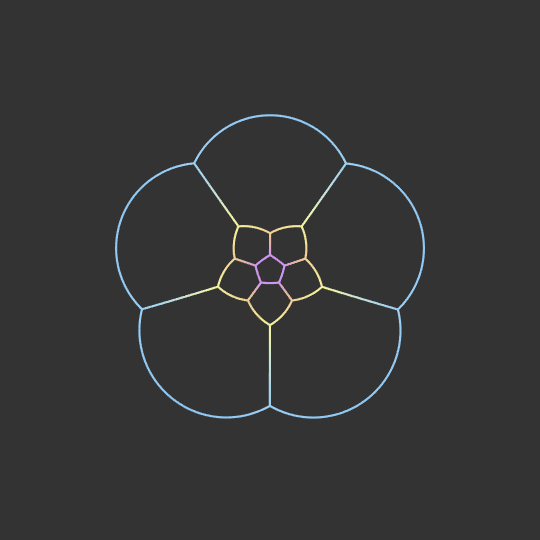
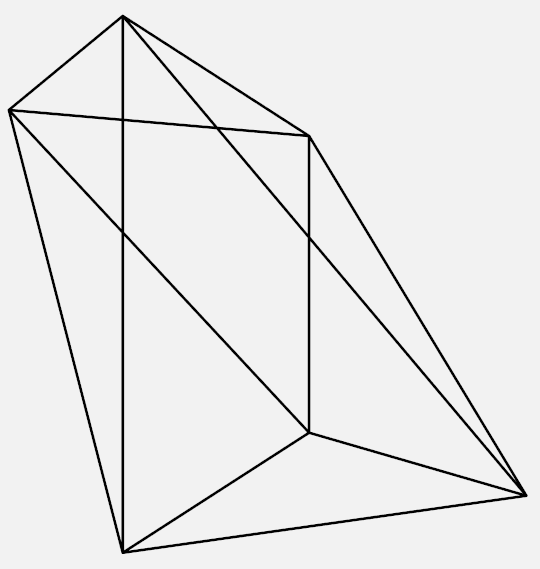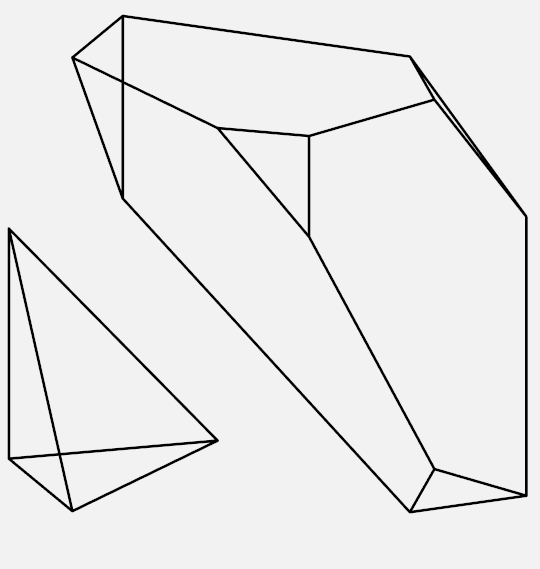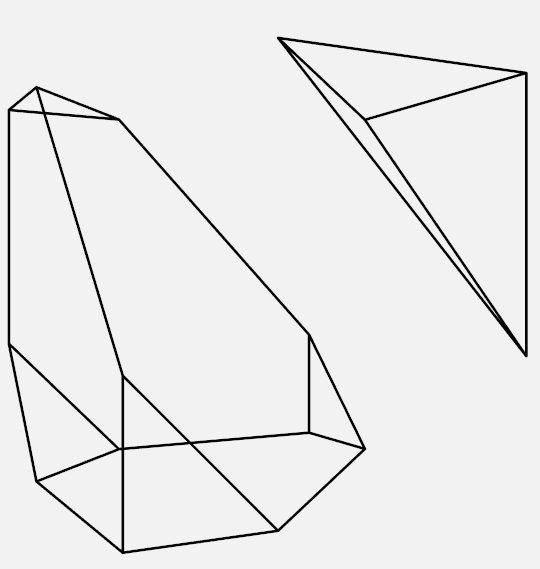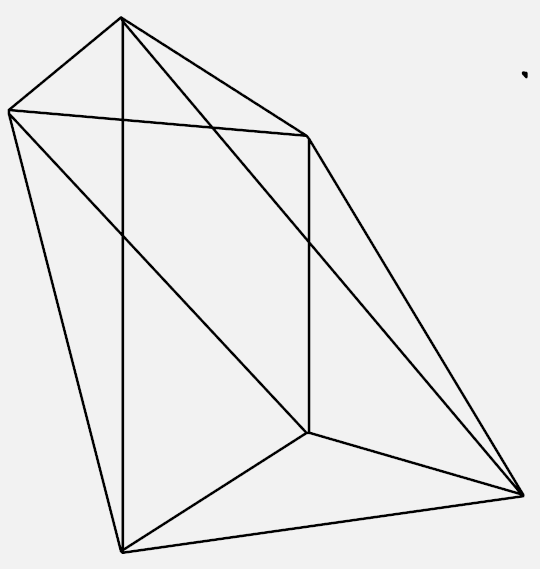
Students, parents, teachers and mathematicians alike will also enjoy visiting Clayton’s website http://shonkwiler.org/, which features stunning mathematical art inspired by the beautiful mathematics that arises in his research and teaching. Some highlights from Clayton’s portfolio are shown below.

If you enjoy what you see, please be sure to Like our Facebook page.